高等数学基础笔记
文章目录

空间解析几何
基本知识
向量的关系
$$ \begin{cases} \vec{\alpha} \cdot \vec{\beta} = |\vec{\alpha}| \cdot |\vec{\beta}| \cdot \cos\theta \Rightarrow \vec{\alpha} \perp \vec{\beta}\ \vec{\alpha} \times \vec{\beta} = |\vec{\alpha}| \cdot |\vec{\beta}| \cdot \sin\theta \Rightarrow \vec{\alpha} // \vec{\beta} \end{cases} $$
向量的坐标运算
$$ \begin{cases} \vec{\alpha} = (a_1, b_1, c_1) \newline \vec{\beta} = (a_2, b_2, c_2) \end{cases} \Longrightarrow \begin{cases} \vec{\alpha} \cdot \vec{\beta} = (a_1a_2, b_1b_2, c_1c_2) \newline \vec{\alpha} \times \vec{\beta} = \begin{vmatrix} i & j & k \newline a_1 & a_2 & a_3 \newline b_1 & b_2 & b_3 \end{vmatrix} (写X左上至右下为正)\newline | \vec{\alpha} \times \vec{\beta} | = a_1a_2 + b_1b_2 + c_1c_2 \newline | \vec{\alpha} | = \sqrt{a_1^2 + b_1^2 + c_1^2} \newline \end{cases} $$
平面方程
$$ \begin{aligned} &平面的一般方程:F=Ax+By+Cz+D=0 \newline &法向量:\vec{\alpha} = (A,B,C) \newline &曲面的法向量:\vec{\alpha} = (\frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z}) \end{aligned} $$
直线方程(平面相交为线)
$$ \begin{aligned} &\text{1.}一般式: \begin{cases} A_1x + B_1y + C_1z + D_1 = 0 \newline A_2x + B_2y + C_2z + D_2 = 0 \end{cases} \newline &\text{2.}对称式(两点式): \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} = \frac{z-z_1}{z_2-z_1} \newline \Rightarrow &经过点(x_1, y_1, z_1),(x_2, y_2, z_2) \newline &方向向量为:[(x_2-x_1), (y_2-y_1), (z_2-z_1)] \newline &\text{3. }参数式: \begin{cases} x = x_1 + \lambda (x_2 - x_1) \newline y = y_1 + \lambda (y_2 - y_1) \newline z = z_1 + \lambda (z_2 - z_1) \end{cases} \end{aligned} $$
定理:直线只需有两个点在平面上,则直线在平面上
旋转曲面方程
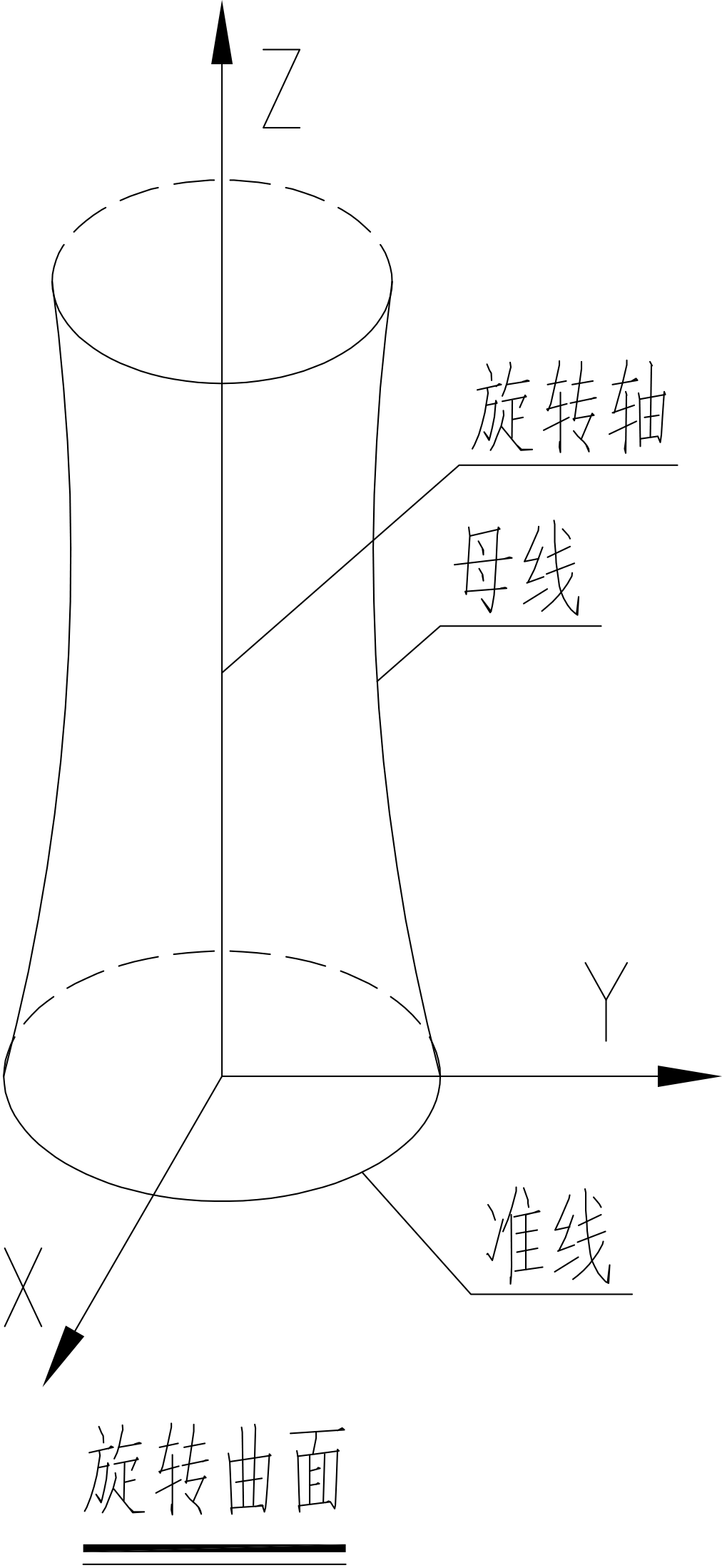
$$ \begin{aligned} &方程: \begin{cases} y^2+z=1\newline x=0 \end{cases} \newline &绕OZ轴旋转以后的方程为:x^2+y^2+z=1 \newline &绕z轴则字母z不变,另一字母变为\sqrt{x^2+y^2} \end{aligned} $$
点到直线/平面的距离
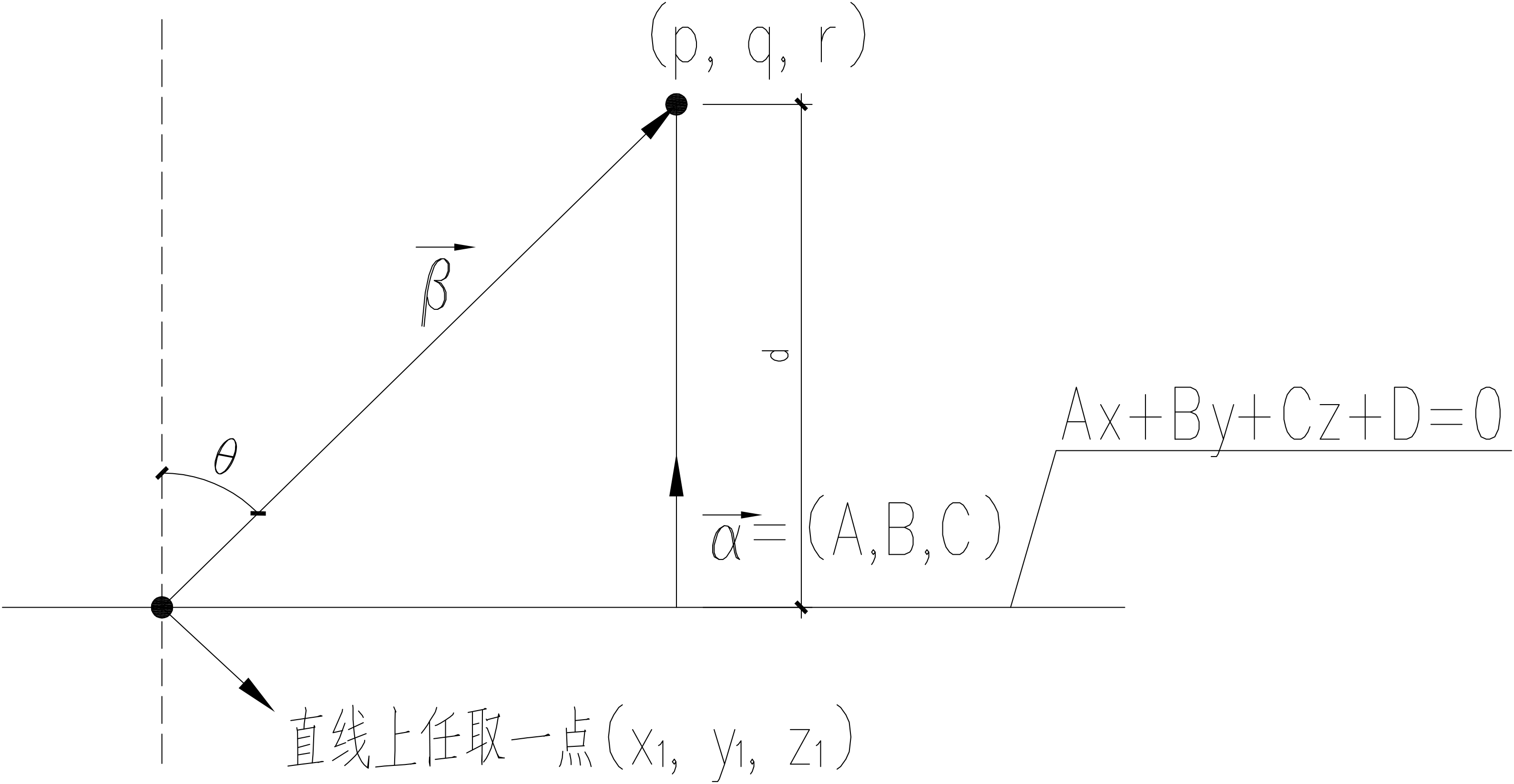
$$ \begin{aligned} &\vec{\alpha}=(A,B,C) \newline &\vec{\beta} = (p-x_1, q-y_1, r-z_1) \newline \Rightarrow & \begin{cases} d = |\vec{\beta}|\cdot \cos \theta = |\vec{\beta}| \frac{\vec{\alpha}\cdot\vec{\beta}}{|\vec{\alpha}||\vec{\beta}|} = \frac{A(p-x_1)+B(q-y_1)+C(r-z_1)}{\sqrt{A^2+B^2+C^2}} \newline Ax_1 + By_1 + Cz_1 + D = 0 \end{cases} \newline \Rightarrow & d = \frac{Ap+Bq+Cr+D}{\sqrt{A^2+B^2+C^2}} \end{aligned} $$
典型例题
例题1
$$ 若向量\vec{\alpha}、\vec{\beta}满足|\vec{\alpha}|=2,|\vec{\beta}|=\sqrt{2},且\vec{\alpha}\cdot\vec{\beta}=2,则|\vec{\alpha}\times\vec{\beta}|=? $$
$$ \begin{aligned} 【解】&设两向量\vec{\alpha}、\vec{\beta}的夹角为\theta,根据\vec{\alpha}\cdot\vec{\beta}=2 \newline \Rightarrow &\cos\theta=\frac{\vec{\alpha}\cdot\vec{\beta}}{|\vec{\alpha}||\vec{\beta}|} = \frac{\sqrt{2}}{2} \newline \Rightarrow &\sin\theta=\frac{\sqrt{2}}{2} \newline \Rightarrow & |\vec{\alpha}\times\vec{\beta}| = |\vec{\alpha}|\cdot|\vec{\beta}|\sin\theta = 2 \end{aligned} $$
微分学
基本知识
基本初等函数
$$ \begin{aligned} 幂函数:&x^{\mu} \newline 指数函数:&a^x \newline 对数函数:&\log{a^x}\newline 三角函数:&\sin{x}、\cos{x}、\tan{x}、\cot{x} \newline 反三角函数:&\arcsin{x}、\arccos{x}、\arctan{x} \end{aligned} $$
无穷小与两个重要极限
$$ 无穷小:\lim \limits_{x\to a}f(x)=0 \begin{cases} 高阶无穷小:\lim \limits_{x\to a}\frac{\beta}{\alpha}=0 \newline 低阶无穷小:\lim \limits_{x\to a}\frac{\beta}{\alpha}=\infty \newline 同阶无穷小:\lim \limits_{x\to a}\frac{\beta}{\alpha} = c(not\ 0)\newline k阶无穷小:\lim \limits_{x\to a}\frac{\beta}{\alpha^k}=c(not\ 0)\newline 等价无穷小:\lim \limits_{x\to a}\frac{\beta}{\alpha}=1\newline \end{cases} $$
$$ 常用等价无穷小: \begin{cases} \sin x \sim x \newline \arcsin x \sim x \newline \tan x \sim x \newline e^x - 1 \sim x \newline a^x-1 \sim x\ln{a}(a>0,a\ne1) \newline \ln(1+x) \sim x \newline \log{a}^{1+x} \sim \frac{x}{\ln a}(a>0,a\ne1) \newline 1-\cos x \sim \frac{1}{2}x^2 \newline (1+\beta x)^{\alpha} -1 \sim \alpha\beta x \newline \end{cases} $$
$$ 两个重要极限: \begin{cases} \lim\limits_{x \to 0}\frac{\sin x}{x} = 1 \newline \lim\limits_{x \to \infty}(1+\frac{1}{x})^x = e \newline \end{cases} $$
洛必达法则
$对于未定式型极限(\frac{0}{0}、\frac{\infty}{\infty})可以采用上下求导的方式求极限:$ $$ \lim\limits_{x \to 0}\frac{f(x)}{F(x)} = \lim\limits_{x \to 0}\frac{f’(x)}{F’(x)} $$
函数的连续性与间断点
$$ 连续 \begin{cases} \text{1. } 在x_0处有定义\newline \text{2. } 左右极限存在且相等\newline \end{cases} $$
$$ 间断点 \begin{cases} 第一类间断点(左右极限均存在) \begin{cases} 可去间断点(在x_0处无定义)\newline 跳跃间断点(左右极限不相等) \end{cases}\newline 第二类(不属于第一类的,包括无穷间断、振荡间断等)\newline \end{cases} $$
基本求导公式与法则
- 基本求导公式:
$$ \begin{aligned} (C)’ &= 0 \newline (x^\mu)’ &= \mu x^{\mu -1} \newline (\sin x)’ &= \cos x \newline (\cos x)’ &= -\sin x \newline (\tan x)’ &= \frac{1}{\cos^2x} \newline (\cot x)’ &= -\frac{1}{\sin^2x} \newline (\sec x)’ &= \sec x \tan x \newline (\csc x)’ &= -\csc x \cot x \newline (a^x)’ &= a^x\ln a \newline (e^x)’ &= e^x \newline (\log{a^x})’ &= \frac{1}{x\ln a} \newline (\ln x)’ &= \frac{1}{x} \newline (\arcsin x)’ &= \frac{1}{\sqrt{1-x^2}} \newline (\arccos x)’ &= -\frac{1}{\sqrt{1-x^2}} \newline (\arctan x)’ &= \frac{1}{1+x^2} \newline (arccot x)’ &= -\frac{1}{1+x^2} \newline \end{aligned} $$
- 和差积商求导法则
$$(u \pm v)’ = u’ \pm v’$$ $$(Cu)’ = Cu’$$ $$(uv)’ = u’v + uv’$$ $$(\frac{u}{v})’ = \frac{u’v - uv’}{v^2}$$
- 复合函数求导
$$ 复合函数F(u),u=t(x); \frac{dF}{dx} = \frac{dF}{du} \frac{du}{dx} $$
$$ 例如:F(u) = 5u,u = x^2; \Rightarrow \frac{dF}{dx} =5 \cdot 2x = 10x $$
- 莱布尼兹公式(高阶求导)
$$(uv)^{(n)} = \displaystyle\sum_{k=0}^nC_n^k u^{(n-k)} v^{(k)} $$
$$ 排列:A_n^k = \frac{!n}{(n-k)!} $$
$$ 组合:C_n^k = \frac{A_n^k}{k!} = \frac{n!}{k!(n-k)!} $$
求导技巧
- 隐函数求导:两边求导
- 取对数后求导
函数的极值
$$ 一阶导数\rightarrow \begin{cases} 单调性 \begin{cases} f’(x)>0 \uparrow \newline f’(x)<0 \downarrow \newline \end{cases} \ 极值点:驻点或不可导点\newline f’(x)=0 \Rightarrow 驻点 \end{cases} $$
$$ 二阶导数\rightarrow \begin{cases} 凹凸性 \begin{cases} f’’(x) > 0 \Rightarrow 凹函数 \newline f’’(x) < 0 \Rightarrow 凸函数 \end{cases} \newline 拐点:f’’(x)=0,凹凸性变化 \end{cases} $$
f(x)与f’(x)的奇偶性相反
全微分
$$\frac{\partial^2Z}{\partial x \partial y} = \frac{\partial^2Z}{\partial y \partial x}$$ $$\Rightarrow Z=f(x,y)先对x求导再对y求导,另一未知量当作常数。 $$
$$ \begin{cases} F(x,y)=0 \newline \frac{dx}{dy} = -\frac{Fx}{Fy} \end{cases} \Rightarrow dz = \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy $$
$$ \begin{cases} F(x,y,z)=0 \newline \frac{\partial z}{\partial x} = -\frac{Fx}{Fz} \newline \frac{\partial z}{\partial y} = -\frac{Fy}{Fz} \newline \end{cases} $$
典型例题
积分学
基本知识
积分的求法
- 与求导相反的基本积分表法
$$ \begin{aligned} \int{kdx} &= kx + C\newline \int{x^\mu dx} &= \frac{x^{\mu+1}}{\mu +1} +C\newline \int\frac{dx}{x}&=\ln|x| +C \newline \int\frac{dx}{1+x^2} &= \arctan x +C\newline \int\frac{dx}{\sqrt{1-x^2}} &= \arcsin x +C\newline \int\cos xdx &= \sin x + C \newline \int\sin xdx &= -\cos x + C\newline \int\frac{dx}{\cos^2x} &= \tan x + C\newline \int\frac{dx}{\sin^2x} &= -\cot x + C\newline \int e^x dx &= e^x +C \newline \int a^xdx &= \frac{a^x}{\ln a} + C\newline \int shxdx &= chx + C \newline \int chxdx &= shx + C \newline \end{aligned} $$
- 第一类换元法(变量代换)
$$ \begin{aligned} 例:&\int\frac{\sin x}{\cos x}dx = \int -\frac{1}{\cos x}d(\cos x) = -ln^{|\cos x|}+C\newline &\int 2\cos 2xdx = \int\cos 2x d2x = \sin 2x + C \newline \end{aligned} $$
- 第二类换元法(将dx的变量x替换)
$$ \begin{aligned} 例:&求\int\sqrt{a^2-x^2}dx\newline &令 x = a\sin t \newline \Rightarrow &原式=\int a^2 \cos t d\sin t = a^2 \int \cos^2 tdt = a^2\int\frac{1+\cos 2t}{2}dt \end{aligned} $$
- 分部积分法
$$ \int udv = uv - \int vdu $$
二重积分的坐标系变换
$$ \begin{cases} &\text{1. } 被积函数中 x = \rho \cos \theta , y = \rho \sin \theta \newline &\text{2. } 面积元素 dxdy = \rho dr d \theta \end{cases} $$
$$ 例:\displaystyle\iint_{D}\frac{dxdy}{1+x^2+y^2}=\int_0^{2\pi}d\theta \int_0^1\frac{1}{1+r^2}rdr $$
线积分
$$ \begin{cases} x = \varphi(t) \newline y = \psi(t) \end{cases} $$
$$ \displaystyle\Rightarrow \int_Lf(x,y)ds = \int_\alpha^\beta f[\varphi(t), \psi(t)]\sqrt{\varphi ‘^2(t)+\psi ‘^2(t)}dt $$
二重积分的几何意义
$$ 二重积分 \iint_Df(x,y)dxdy \rightarrow 某一包围区域的体积 $$
例:
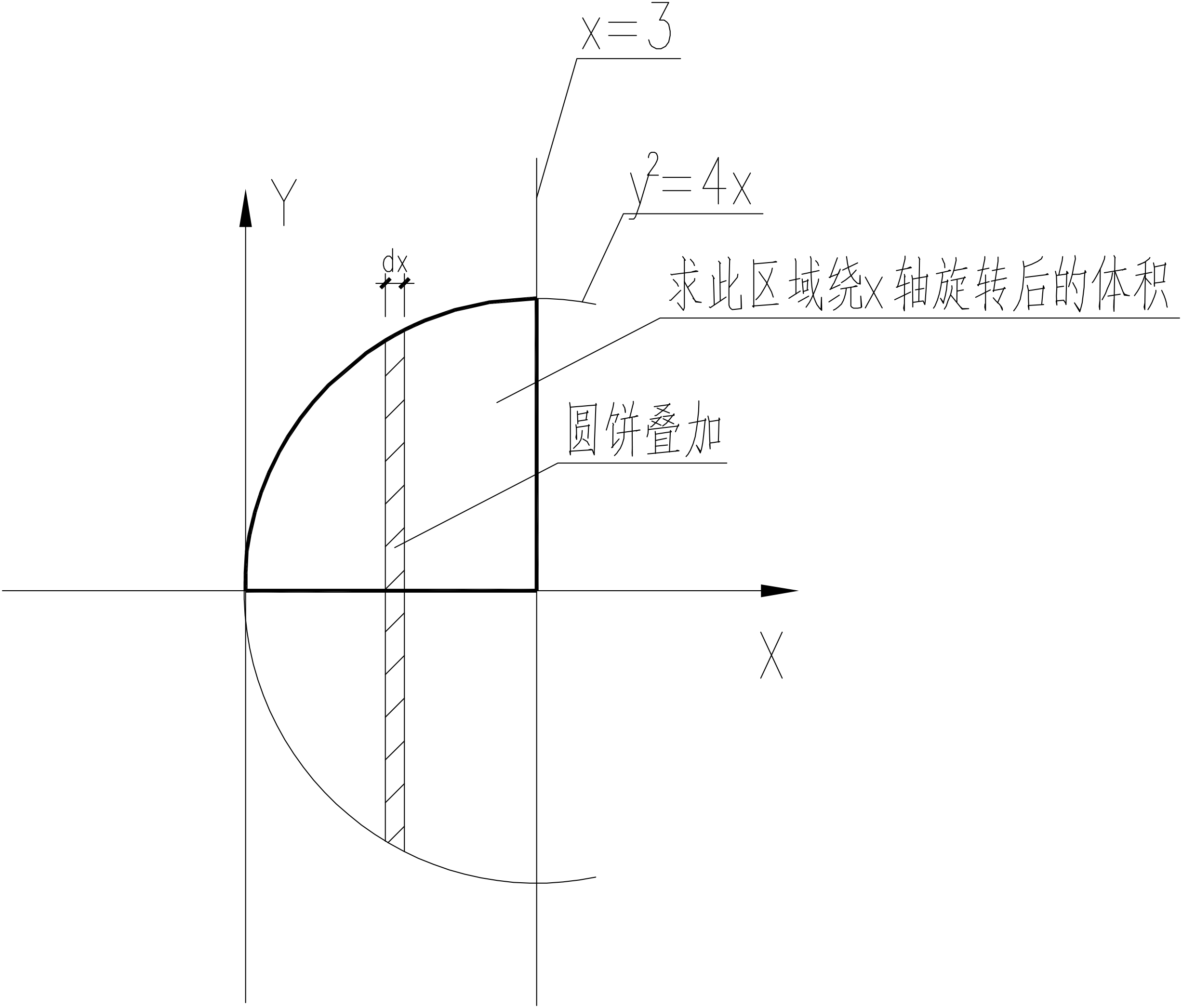
$$ \iint_Ddxdy = \int_0^3 \pi y^2dx=\int_0^3 \pi 4xdx $$
典型例题
无穷级数
基本知识
基本概念
$$ S_n=\displaystyle\sum_{i=1}^nu_i \rightarrow 割圆术、等比数列和等 $$
$$ \lim\limits_{n \to \infty}S_n = S \begin{cases} \xrightarrow{是}收敛 \newline \xrightarrow{是}发散 \end{cases} $$
$$ 基本性质 \begin{cases} \lim\limits_{n \to \infty}\sum u_n = S \Rightarrow \lim\limits_{n \to \infty}\sum ku_n = kS \newline \sigma = \lim\limits_{n \to \infty}\sum v_n \Rightarrow \lim\limits_{n \to \infty}\sum{u_n + v_n} = S + \sigma \newline 增减项数不变 \newline \lim\limits_{n \to \infty}u_n = 0 \rightarrow 单项极限为零 \end{cases} $$
调和级数(发散)
$$ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+…+\frac{1}{n}+… $$
p级数
$$ 1+\frac{1}{2^p}+\frac{1}{3^p}+\frac{1}{4^p}+…+\frac{1}{n^p}+… $$
$$ \Rightarrow \begin{cases} p\leq 1时发散 \newline p > 1时收敛 \end{cases} $$
幂级数
$$ \begin{aligned} &定义与概念:\lim\limits_{n=0}^{\infty}a_n(x-c)^n \newline &收敛半径:R=\lim\limits_{n \to \infty}|\frac{a_n}{a_{n+1}}|=\frac{1}{\rho}\newline &展开 e^x = \displaystyle\sum_{n=0}^{\infty}\frac{x^n}{n!}\ (注意:0! = 1)\newline &常用的一个幂函数的和:x^0+x^1+…+x^n+…=\frac{1}{1-x} \end{aligned} $$
绝对收敛(绝对值收敛)
$$ \begin{aligned} \displaystyle\sum_{n=1}^{\infty}a_n 收敛且 \displaystyle\sum_{n=1}^{\infty}|a_n| 也收敛 \rightarrow 绝对收敛 \newline \displaystyle\sum_{n=1}^{\infty}a_n 收敛且 \displaystyle\sum_{n=1}^{\infty}|a_n| 发散 \rightarrow 条件收敛 \newline 交错级数\displaystyle\sum_{n=1}^{\infty}(-1)^{n-1}u_n的收敛条件 \rightarrow \begin{cases} u_n \geq u_{n+1} \newline \lim\limits_{n \to \infty}u_n = 0 \end{cases} \end{aligned} $$
泰勒级数与麦克劳林级数
$$ \begin{aligned} 泰勒级数:f(x) = &f(x_0) + f’(x_0)(x-x_0)+\frac{f’’(x_0)(x-x_0)^2}{2!}+…\newline &+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!}+…\newline &\displaystyle x_0 = 0 时 \rightarrow 麦克劳林级数 \end{aligned} $$
典型例题
常微分方程
基本知识
可分离变量的微分方程求法
$$ 可以写成g(y)dy=f(x)dx的微分方程,两边积分后代入边界条件即可求得解 $$
齐次方程
$$ \frac{dy}{dx}=f(x,y) \rightarrow 可以写成\frac{y}{x}的函数,即f(x,y) = \varphi (\frac{y}{x}) $$
$$ \begin{aligned} 例:&求y^2+x^2\frac{dy}{dx} = xy\frac{dy}{dx} \newline \Rightarrow &\frac{dy}{dx} = \frac{y^2}{xy-x^2} = \frac{(\frac{y}{x})^2}{(\frac{y}{x})-1} \newline 令&u = \frac{y}{x} \Rightarrow \begin{cases} y = ux \newline \frac{dy}{dx} = u+x\frac{du}{dx} \end{cases}\newline \Rightarrow &原式变为 u+x\frac{du}{dx} = \frac{u^2}{u-1} \newline \Rightarrow &x\frac{du}{dx} = \frac{u}{u-1} \newline \Rightarrow &(1-\frac{1}{u})du = \frac{1}{x}dx \newline 两端积分 \Rightarrow &u - \ln^{|u|} + C = ln^{|x|} \newline 用u = \frac{y}{x}代换回来 \Rightarrow &\ln^{|y|} = \frac{y}{x} + C \end{aligned} $$
线性微分方程
$$ \begin{aligned} 非齐次线性微分方程:&\frac{dy}{dx} + P(x)y = Q(x) \newline 即:&y’ + P(x)y = Q(x) \newline 齐次线性微分方程:&\frac{dy}{dx} + P(x)y = 0 \newline 即:&y’ + P(x)y = 0 \newline 求解步骤: &\begin{cases} 先求齐次通解 \newline 用u(x)替代常数C \newline 求得u(x) \newline u 回代齐次通解 \end{cases} \newline \end{aligned} $$
二阶常系数齐次微分方程
$$ \begin{aligned} &求y’’ + py’+qy = 0 的通解:\newline &\text{1. } 特征方程为r^2+pr+q=0 \newline &\text{2. } 求特征方程的两个根r_1、r_2 \newline &\text{3. } 根据r_1、r_2判断通解的形式 \newline &\rightarrow \begin{cases} 不相等实根r_1,r_2:y=C_1e^{r_1x}+C_2e^{r_2x} \newline r_1=r_2:y=(C_1+C_2x)e^{r_1x}\newline 共轭复根r_{1,2}=\alpha \pm i\beta:y= e^{\alpha x}(C_1 \cos \beta x + C_2 \sin \beta x) \end{cases} \end{aligned} $$
二阶常系数非齐次微分方程
$$ 求y’’ + P(x)y’+Q(x)y = f(x) 的通解: $$
$$ 设 \begin{cases} y^*(x)是常系数微分方程的一个特解,\newline Y(x)是对应的齐次方程的通解 \end{cases} $$
$$ \Rightarrow y = Y(x) + y^*(x) $$
$$ 对f(x) = P_m(x)e^{\lambda x}形式判断【Q_m(x)是与P_m(x)同次的多项式】: $$
$$ \Rightarrow y^*=x^kQ_m(x)e^{\lambda x} \rightarrow \begin{cases} \lambda 是特征方程的根\Rightarrow k=0 \newline \lambda 是特征方程的单根\Rightarrow k=1 \newline \lambda 不是特征方程的根\Rightarrow k=2 \newline \end{cases} $$
$$ \Rightarrow 得出特解形式后将特解代回原方程,对比双边系数。 $$
典型例题
线性代数
概率与数理统计
文章作者 Evan Yu
上次更新 2019-10-26